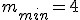Materiały » Zadania 
Pokaż rozwiązanie »
Zadanie 13
Matcyfrzak zapisał funkcję m(x)=(x–1)(x–2)(x–3)(x–4)+5, a Wymierniak funkcję w(x)=(x–5)(x–6)(x–7)(x–8)+5. Można stwierdzić, że:| TAK | NIE | ||
| A. obie funkcje są cały czas dodatnie | |||
| B. jedna z funkcji ma przedziały ujemne | |||
| C. najmniejsza wartość obu funkcji jest taka sama | |||
| D. obie funkcje mają oś symetrii |
Pokaż rozwiązanie »
![m(x)=[(x-1)(x-4)]\cdot [(x-2)(x-3)]+5=[(x^2-5x)+4][(x^2-5x)+6]+5=[(x^2-5x)^2+6(x^2-5x)+4(x^2-5x)=24]+5=](../../MATERIALY/latexrender/pictures/937e3bf4ba8a7da9ab6572942919d418.gif "m(x)=[(x-1)(x-4)]\cdot [(x-2)(x-3)]+5=[(x^2-5x)+4][(x^2-5x)+6]+5=[(x^2-5x)^2+6(x^2-5x)+4(x^2-5x)=24]+5=")
![=[(x^2-5x)^2+10(x^2-5x)+24]+5=[(x^2-5x)+5]^2-1+5=\underbrace{(x^2-5x+5)^2}_{\ge 0}+4](../../MATERIALY/latexrender/pictures/9820b3817caf5f23fff334a590f14ef1.gif "=[(x^2-5x)^2+10(x^2-5x)+24]+5=[(x^2-5x)+5]^2-1+5=\underbrace{(x^2-5x+5)^2}_{\ge 0}+4")
