Materiały » Zadania 
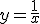przecięto dwiema prostymi 
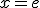oraz 
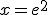. Pole ograniczone prostymi, osią układu i funkcją jest równe:
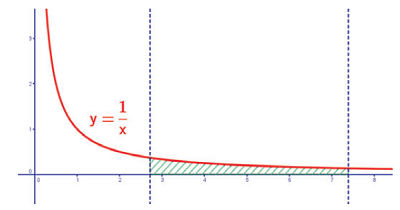
Pokaż rozwiązanie »
Zadanie 39
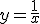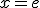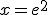Funkcję homograficzną przecięto dwiema prostymi oraz . Pole ograniczone prostymi, osią układu i funkcją jest równe:
| TAK | NIE | ||
A. ![1\;[j^2]](../../MATERIALY/latexrender/pictures/1d1a166856448257bd95aa16a6c9337d.gif "1\;[j^2]") | |||
B. ![2\sqrt{e}\;[j^2]](../../MATERIALY/latexrender/pictures/a050462a164eaeec4a8d4fed0b3f5d5e.gif "2\sqrt{e}\;[j^2]") | |||
C. ![e\;[j^2]](../../MATERIALY/latexrender/pictures/09d2efd93737ae31c6fd36d54530f7d6.gif "e\;[j^2]") | |||
D. ![\frac1e-\frac1{e^2}\;[j^2]](../../MATERIALY/latexrender/pictures/0abe9af9ecd91aae121e31869ec5ea37.gif "\frac1e-\frac1{e^2}\;[j^2]") |
Pokaż rozwiązanie »
![\int_{e}^{e^2}{ }\frac{1}{x}\;dx=[ln|x|]_e^{e^2}=ln|e^2|-ln|e|=2-1=1\;j^2](../../MATERIALY/latexrender/pictures/9f92e88080c4ffae9535ec698c0fdc46.gif "\int_{e}^{e^2}{ }\frac{1}{x}\;dx=[ln|x|]_e^{e^2}=ln|e^2|-ln|e|=2-1=1\;j^2")
