Materiały » Zadania 
Pokaż rozwiązanie »
Zadanie 262
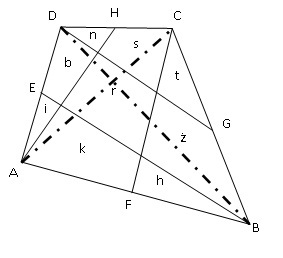
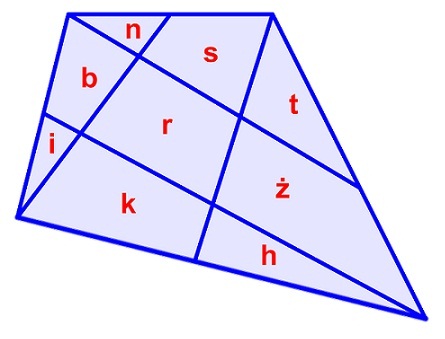
Różniczka zazdroszcząc koleżance podzieliła swój ogród na 9 części w ten sposób, że prowadziła z każdego wierzchołka linię, która przecinała jeden z naprzeciwległych boków w połowie (patrz rys.). W każdej części ma zamiar hodować również inny rodzaj kwiatów. W części środkowej r – róże, w pozostałych: b – bratki, n – niezapominajki, k – konwalie, s – stokrotki, i – irysy, t – tulipany, ż – żonkile, h – hiacynty, P – powierzchnia całego ogrodu. Wynika z tego, że powierzchnia, którą zajmują określone kwiaty, ma następujące własności:
| TAK | NIE | ||
| A. P=5r | |||
| B. i+b+n=n+s+t | |||
| C. r= 13 (b+r+ż) | |||
| D. i+n+t+h=r |
Pokaż rozwiązanie »
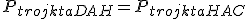oraz 
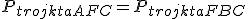. Równości te wynikają z równych długości podstaw i wysokości trójkątów. Oznacza to, że 
∙ 
∙
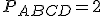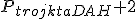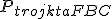. Podstawiając określone obszary, można otrzymać równanie:
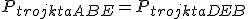oraz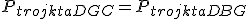 
, czyli 
∙
∙
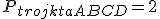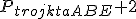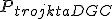, więc n+b+i+s+r+k+t+ż+h=2∙(i+k+n)+2∙(n+s+t)
