A_07

Już wiesz, jak skonstruować okrąg przechodzący przez trzy dowolne punkty. Jeśli punkty te będą wierzchołkami trójkąta, wówczas okrąg ten nazywamy okręgiem opisanym na trójkącie, albo mówimy, że trójkąt jest wpisany w okrąg.

Nie sądzę, aby kiedykolwiek przyszło Ci do głowy narysować tak trójkąt, aby jego wierzchołki leżały na jednej prostej. Pewnie w Twoim odczuciu nie byłby to trójkąt.
W programie Cabri jest to jednak możliwe, gdyż nie ma żadnych ograniczeń co do położenia obiektów na ekranie.
Spróbuj zatem w poniższym aplecie przemieścić myszą tak wierzchołek C trójkąta, aby chociaż w przybliżeniu leżał on na odcinku AB, lub na jego przedłużeniu.

Jak zachowują się wówczas symetralne boków trójkąta? (42)
Co stało się z okręgiem? (43)
Czy to możliwe by uległ on "wyprostowaniu".?
A gdzie według Ciebie znajduje się wówczas jego środek? (44)

Zauważ, że zbliżając się punktem C do prostej AB symetralne par punktów AB, AC i BC stają się równoległe. Zatem nie przecinaja się.
Dlatego też środek okręgu, który jest zawsze punktem przecięcia symetralnych też oddala się w nieskończoność, a jego promień wydłuża się do nieskończoności.

Taka sytuacja przypomina nam widok równoległych szyn pewnego toru kolejowego, na które kolejowego na które patrzymy stojąc na tym torze. Niby nie powinny się zetknąć, bo odległość między nimi jest zawsze taka sama a jednak widzimy, że się przecinają.
Kazdy malarz narysuje je na obrazie jako proste stykające się. Punkt ich przecięcia malarze nazywają środkiem perspektywy.

Matematycy na bazie tego założenia, że dwie proste w nieskończoności przecinają się zbudowali cały dział matematyki, nazywany geometrią rzutową. Punkt ich przecięcia nazwali "punktem niewłasciwym" i oznaczyli symbolem .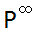

Wrócmy do trójkąta ABC, którego wierzchołki nie są współliniowe. Narysujmy w nim symetralne par punktów AB, AC i BC oraz dwusieczne jego kątów wewnętrznych - patrz kolejny aplet.
Gdzie przecinają się te dwusieczne z symetralnymi boków przeciwległych do ich kątów? (45)
Czy tak jest zawsze? Poruszaj wierzchołkami trójkąta by się o tym przekonać.

Pewnie dziwisz się, dlaczego tak dzieje. Formalny dowód tego faktu przeprowadzimy w jednej z kolejnych lekcji.